본래 cs231n 3강은 Loss function (손실 함수)와 Optimization (최적화)에 대한 내용을 다루지만
내용이 너무 방대한 관계로 3강은 두 포스팅으로 나누어서 작성할려고 한다.
손실 함수 (Loss function)
지난 강의에선 f(x, W) = Wx + b 라는 형태의 선형 분류기를 보여주고 마무리가 되었는데
이번 강의에선 W 즉, 가중치를 판단하는 방법과 고르는 방법을 알려준다.
가중치의 값이 데이터를 올바르게 분류하고 있는지를 판단할려면 손실 함수를 사용하여 판단하여야 한다.

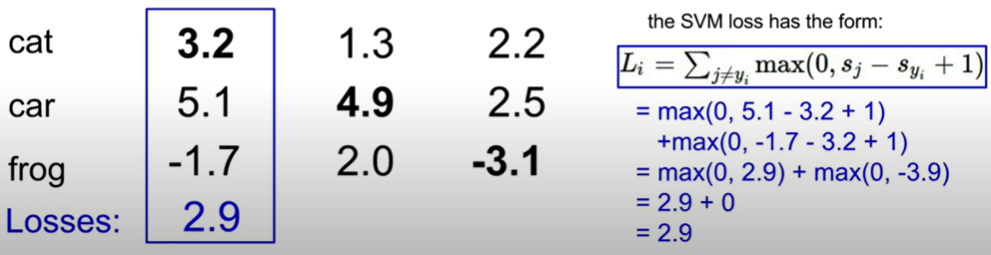
위의 사진은 선형 분류기를 통해 얻어낸 각 카테고리 별의 점수를 포함하고 있고 우측에는 손실 함수의 기본적인 형태를 알려주고 있다.
손실 함수는 선형 분류기의 점수 값과 맞는 라벨의 값을 입력을 받고 특정한 함수를 통해 손실 값을 도출해낸다.
입력 받은 각각의 이미지마다 손실 값을 도출하고 더한 다음 평균을 내는 것으로 우리는 최종적인 손실 값을 구하는 것이다.
Multiclass SVM (다중 클래스 서포트 벡터 머신)
Multiclass SVM은 손실 함수의 종류 중 하나이다. 해당 손실 함수는 이미지 분류에 쓰이기 좋은 손실 함수라고 한다.
Multiclass SVM은 입력 받은 이미지와 다른 라벨의 점수와 맞는 라벨의 점수를 비교해서 손실 값을 도출해낸다.
예를 들어 고양이 사진을 입력했을 때 고양이라고 측정한 점수와 자동차, 개구리라고 측정한 점수를 비교하는 것이다.
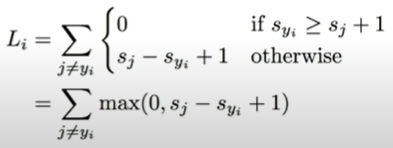
해당 식을 해석해보자면 올바른 라벨을 고른 점수 (s_y_i)와 올바르지 않은 라벨을 고른 점수(s_j)에 1을 더하여 비교하여 올바른 라벨을 고른 점수가 더 크다면 0을 값으로 내놓고 아니라면 그 두개의 차를 내놓은다. 해당 절차를 정답 라벨을 제외한 모든 라벨에서 진행하고 더한다.
설명을 더하자면 조건식으로 쓴 수식과 최댓값 함수를 이용하여 쓴 수식이 둘 다 있는데 둘 다 같은 의미이다.
어차피 s_j + 1이 더 작다면 두 점수의 차를 구했을 때 무조건적으로 음수값이 나오기에 0을 값으로 해야한다.

Multiclass SVM을 그래프로 그려보았을 때 꺽인 형태, 즉 hinge 모양과 같다고 해서 hinge loss라고도 불린다.
이후 Multiclass SVM의 특성을 알아볼수 있는 질문과 답변을 몇가지 알려주었다.
1. s_y_i의 값이 가장 크다고 가정했을 때 해당 값을 조절했을 때 손실 값의 차이가 날까?
-> 차이가 존재하지 않는다. SVM은 점수 간의 상대적인 차이를 보는 것이기 때문에 s_j와 1 이상 차이가 난다면 결과는 달라지지 않는다.
2. Multiclass SVM 손실 값의 최솟값, 최댓값은 무엇일까?
-> 최솟값은 0 그리고 최댓값은 무한이다.
3. 가중치를 처음 설정할 때는 랜덤으로 숫자를 부여하는데 이때 선형 분류기는 모든 카테고리에 대하여 0에 가까운 점수를 도출해내는데 이럴 때 SVM의 손실 값은 얼마일까?
-> N이 카테고리의 갯수를 나타낸다고 가정했을 때 N-1이다.
-> 이유는 모든 카테고리에서 s_y_i - s_j + 1의 값만 얻을텐데 s의 값은 서로 0으로 비슷하기에 1만 계속 결과값으로 나와 더해질 것이다. 올바른 라벨은 제외하고 반복하기에 N-1이 손실 값으로 나온다.
-> 해당 특성은 디버깅 전략으로 유용하게 쓰일 수 있는데 만약 내가 모델을 구현하고 가중치를 초기에 랜덤으로 세팅했다고 하자. 그러면 손실 값은 N-1에 근접하게 나와야 내가 오류없이 잘 코드를 짰다는 것이다.
4. SVM은 올바른 라벨에 대하여 손실 값을 계산하지 않는데 만약 계산한다면 손실 값에 어떠한 변화가 있을까?
-> s_y_i = s_j이기에 1이라는 값을 내놓을 것이기에 원래 손실 값에 1이 더해진 값이 나올 것이다.
5. 합이 아니라 평균을 사용했다면 어떤 차이가 있을까?
-> 아까도 말했지만 상대적인 차이를 보는 것이기에 합이 아니라 평균을 사용해도 상관이 없다.
6. SVM을 제곱해서 사용하면 어떤 차이가 있을까?
-> hinge loss는 선형적인 형태이기에 제곱을 하면 비선형적인 형태로 바뀐다. 그렇다면 손실 함수 자체가 바뀌기에 의미 자체가 달라진다.
-> 제곱 SVM은 손실 값이 큰 것은 더욱 크게 해줄 것이고 작은 것은 더욱 작게 해줄 것이다. 그렇기에 내가 해결하고자 하는 문제의 상황에 따라 제곱 SVM이 더욱 효과적인 손실 함수가 될 수도 있다.
7. 만약 손실 값이 0이 나오는 가중치 값을 찾았다고 가정했을 때 해당 가중치는 유일한 값일까?
-> 아니다. 무수히 많은 가중치 값이 손실 값을 0으로 만들 것이고 당장 2W 만을 생각해도 2W도 손실 값은 0이다.
Multiclass SVM 파이썬 코드
def L_i_vectorized(x, y, W):
scores = W.dot(x)
margins = np.maximum(0, scores - scores[y] + 1)
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
margins[y] = 0 이라는 코드를 통해 맞는 라벨의 손실 값은 0으로 수동적으로 변화시켜 굳이 반복문을 돌리는 것이 아닌
vectorized 된 코드를 구현할 수 있는 것이다.
정규화 (Regularization)
우리가 원하는 것은 손실 값을 0으로 만드는 것이 아니다. 지금 손실 값이 0이라는 것은 구해진 가중치 값은 학습용 데이터에만 맞게 조정된 값이므로 과적합 문제를 불러일으킨다.
해당 문제를 방지하기 위해 우리는 정규화라는 것을 한다.
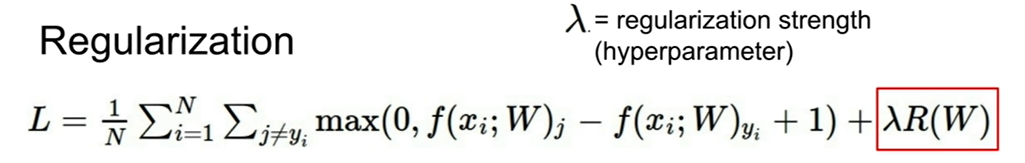
정규화 상수에는 λ가 포함되어 있는데 해당 λ값은 하이퍼파라미터의 일부로 튜닝을 통해 적절한 값을 찾아줘야 한다.
λ값이 0에 가까울수록 정규화의 효과는 줄어들고 λ값이 커질수록 정규화의 효과는 더욱 커진다.

수많은 정규화 방법들이 있지만 3강에서는 L2와 L1 정규화에 대해 주로 다뤘다.
L2 정규화는 가중치가 모든 x에 퍼져있도록 하는 것이고 L1 정규화는 sparse 하게 즉 0이 많이 포함되어있는 가중치를 만드는 것이라고 설명했다.
필자는 강의 설명만으로는 L2와 L1의 차이와 정규화의 작동 원리에 대해 이해가 가지 않아 검색을 통해 정보를 더 모았다.
L2 Regularization vs. L1 Regularization
먼저 정규화를 설명하기 전에 필요한 몇가지 지식 먼저 끄적여볼려고 한다.

norm이란 벡터의 크기 혹은 벡터 간의 거리를 뜻한다.
norm에는 L1 norm 그리고 L2 norm이 존재하는데 L1 norm은 맨해튼 거리를 이용한 것이고 L2 norm은 하나의 최단 거리를 표현한다. L1 norm은 맨해튼 거리를 사용하기에 여러 개의 경로가 존재한다.

해당 norm을 통해 알수있는 것은 L1 norm은 여러 가지의 경로를 가지고 있으며 그렇기에 특정 특성을 0으로 만드는 것이 가능하다. 위의 사진에서 파란 선은 지그재그로 가지만 빨간 선은 일직선으로 가 한번만 꺽어 목표를 향해 간다. 이러한 것을 feature selection 이라고 한다.
위의 지식을 가지고 정규화가 어떻게 작동하는지부터 이해를 해보자.

L2 정규화는 가중치의 제곱의 합을 손실 함수에 더해주고 L1 정규화는 가중치의 절댓값의 합을 손실 함수에 더해준다.
더해지는 정규화 상수의 값은 손실 값을 증가시킨다. 그 의미는 본디 가중치가 일으키는 손실보다 더 손실을 크게 만든다는 것인데 이러한 현상을 penalty를 부여한다고 한다.
해당 penalty를 이길 만큼 가중치를 줄여야되기에 정규화가 가중치를 줄여 모델을 더욱 심플하게 만드는 것이다.
아까 위에서 말했듯이 L2 정규화는 가중치가 모든 x에 고루 퍼져있도록 하는 것이고 L1 정규화는 몇몇 x의 가중치를 0으로 만드는 것이라고 했다. 왜 그러는 것일까?

w_1이나 w_2나 선형 분류기에서는 똑같은 값을 도출해낸다.하지만 두개의 가중치의 L1 norm과 L2 norm을 구한다면 어떨까?
L1 norm
$$\left|w_1\right|= 1 + 0 + 0 + 0 = 1$$
$$\left|w_2\right|= 0.25 + 0.25 + 0.25 + 0.25 = 1$$
L2 norm
$$w_1^2 = 1^2 + 0^2 + 0^2 + 0^2 = 1$$
$$w_2^2 = 0.25^2 + 0.25^2 + 0.25^2 + 0.25^2 = 0.5 $$
보다시피 L2 norm이 가중치가 더 퍼져있는 경우에 패널티를 적게 부여한다. 그렇기에 L2 정규화는 퍼져있는 가중치를 선호하는 것이고 L1 정규화가 sparse한 가중치를 더 선호하는 것이다.
Multinomial Logistic Regression (Softmax) 손실 함수
Multiclass SVM에서는 스코어 간 차이에 중점을 두고 스코어 자체 값에 대한 의미를 부여하지 않았지만 softmax는 스코어에 대한 해석을 추가한 손실 함수이다.

먼저 스코어들을 양수로 만들기 위해 각 스코어를 지수를 취해주고 지수를 취한 스코어들의 합으로 나누어준다. 그러면 모든 스코어들의 합은 1이 되고 각 스코어는 0에서 1 사이인 확률 분포가 만들어진다.
그렇게 나온 값은 입력된 이미지가 각 카테고리가 맞을 확률이 된다.
이후 -log를 취해주어 손실 값을 구해낸다.
여기서 -log를 취해주는 이유는 로그 함수가 단조로운 함수이기에 손실 값을 표현하기에 적당하고 음수 부호를 붙인 이유는 우리의 목표는 올바른 라벨의 스코어의 확률이 1에 가까워야 하기에 결과값이 나쁠수록 손실 값이 커져야하기에 상승하는 로그 함수를 음수 부호를 붙여 하락하는 함수로 만든 것이다.

이후 Multiclass SVM과 같은 질문들이 나왔다.
1. softmax 손실 함수의 최솟값과 최댓값은?
-> 최솟값은 0, 최댓값은 무한이다. 만약 확률의 최솟값인 0이 나온다면 -log(0) = 무한이고 최댓값인 1이 나오면 -log(1) = 0 이기 때문이다.
2. 가중치를 처음 설정할 때는 랜덤으로 숫자를 부여하는데 이때 선형 분류기는 모든 카테고리에 대하여 0에 가까운 점수를 도출해내는데 이럴 때 softmax의 손실 값은 얼마일까?
-> 확률 분포로 변환 했을 때 모든 스코어는 비슷한 확률을 가지고 있을 것이다. 그렇기에 모든 스코어의 확률은 N이 클래스의 갯수라고 가정했을 때 1/N이 될 것이다. 즉, 손실 값은 -log(1/N) = log(N)이 될 것이다.
마무리하며
휴가를 나갔다오고 오랜만에 다시 들은 강의여서 그런지 아니면 그냥 내용 자체가 어려웠는지 모르겠지만 이번 강의는 이해하기 너무 어려웠고 추가적인 정보 탐색이 거의 필수였다. 그렇지만 그래도 포기하지 않으면 결국은 모든 내용을 이해하고 포스팅을 작성하는데 까지 이르렀다.
최적화도 얼른 강의를 마무리해 포스팅을 적어보도록 하겠다!
전역까지 339일 남았는데 얼른 cs231n 강의를 마치고 다음 단계로 넘어가 더욱 실력을 키워야겠다.
'Deep Learning > CS231n' 카테고리의 다른 글
| [3-2강] Optimization (0) | 2024.05.12 |
|---|---|
| [과제 1] K-Nearest Neighbor (KNN) (2) | 2024.04.25 |
| [2강] Image Classification (0) | 2024.04.16 |
| [1강] Introduction to Convolutional Neural Networks for Visual Recognition (0) | 2024.04.10 |



